Filtracja wykorzystująca dyskretną transformatę Fouriera (DFT) jest związana z procesem przetwarzania sygnału w dziedzinie czasu w celu uzyskania pożądanych zmian w widmie sygnału oryginalnego. Filtr cyfrowy może być dedykowanym układem cyfrowym lub programowalnym procesorem albo programem komputerowym. Rozwiązania takie, w przeciwieństwie do filtrów analogowych, są stosunkowo łatwe do zbudowania i implementacji. Nie zmieniają charakterystyk w funkcji temperatury ani wilgotności, nie starzeją się ani nie zależą od producenta ani od serii i daty produkcji, są też dużo tańsze w produkcji.
Rozróżnia się dwa podstawowe typy filtrów cyfrowych:
- FIR (Finite Impulse Response ) - filtry o skońcoznej odpowiedzi impulsowej znane też jako filtry MA (Moving Arage) o ruchomej średniej, lub filtry nierekurencyjne. Odpowiedź tego filtra zależy od bieżącej i poprzednich wartości wejściowych.
- IIR (Infinite Impulse Response) - filtry o nieskończonej odpowiedzi impulsowej znane też jako filtry ARMA (Autoregressive Moving Average) autoregresyjne z ruchomą średnią, lub filtry rekurencyjne. Odpowiedź filtra zależy od bieżącej i poprzednich wartości wejściowych - jak dla FIR - oraz bieżących i poprzednich wartości wyjściowych.
- Filtry FIR są: łatwiejsze do projektowania i zastosowania, są z natury stabilne i odporne na błędy zaokrągleń (odpowiedź filtra po skończonym czasie osiąga wartość zero), mają liniową fazę, działają jednak wolniej, wymagają większej pamięci i większej liczby współczynników.
- Filtry IIR są: trudniejsze do projektowania i zastosowania, mogą być niestabilne a błędy zaokrągleń mogą się kumulować, przesunięcie fazowe jest nieliniowe, działają jednak znacznie szybciej i wymagają mniej współczynników (niższy rząd filtrów)
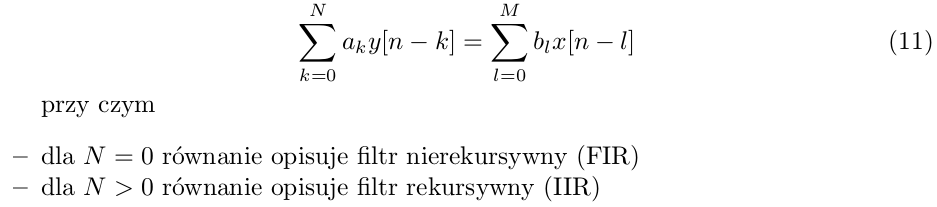
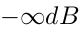 w paśmie zaporowym. Rzeczywisty filtr posiada jednak skończone tłumienie a jego charakterystyka może zawierać zafalowania w pasmach przepustowych i zaporowych. Zwykle, jeśli jest to filtr pasmowy, dąży się do tego aby zafalowania były symetryczne. Wartość tłumienia można określić korzystając z następującego wzoru:
w paśmie zaporowym. Rzeczywisty filtr posiada jednak skończone tłumienie a jego charakterystyka może zawierać zafalowania w pasmach przepustowych i zaporowych. Zwykle, jeśli jest to filtr pasmowy, dąży się do tego aby zafalowania były symetryczne. Wartość tłumienia można określić korzystając z następującego wzoru:
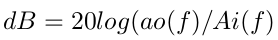
Znanych jest wiele metod projektowania filtrów cyfrowych. Filtry FIR można projektować korzystając np. z metody okienkowej zwanej też klasyczną. Zadanie polega na takim doborze kształtu funkcji wycinającej (okienkowej) aby dla zadanej charakterystyki częstotliwościowej filtra uzyskać jak najmniejszą liczbę współczynników (taps - rząd filtra). Nie jest to metoda najlepsza, lepsze wyniki (niższy rząd filtra) można znaleźć korzystając np. z metody Parksa i McClellana opartej o algorytm Remeza. Algorytm ten śledzi, na bieżąco, różnicę między żądaną a aktualną charakterystyką w całym zakresie częstotliwościowym filtra, dając w wyniku filtr o stałym poziomie tętnień w paśmie przepustowym i paśmie zaporowym. W porównaniu do metody okienkowej wymagany jest długi czas projektowania, złożoność obliczeniowa i brak gwarancji zbieżności algorytmu.
Projektowanie filtra typu IIR jest zadaniem o wiele bardziej skomplikowanym niż projektowanie FIR (w filtrach IIR amplituda odpowiedzi impulsowej narasta z czasem a w filtrach FIR dąży do zera). Wyznaczenie charakterystyki częstotliwościowej filtra IIR na podstawie znanych (przyjętych) wartości nie jest problemem (zadanie wprost). Problem pojawia się gdy należy wyznaczyć współczynniki filtra na podstawie charakterystyki częstotliwościowej (zadanie odwrotne). Nie jest znana metoda takiego rozwiązania i stosowane są metody przybliżone np. metoda niezmienności odpowiedzi impulsowej, zakładająca istnienie, odpowiadającego projektowanemu filtrowi cyfrowemu, filtra analogowego o takiej samej odpowiedzi impulsowej. Projektowanie sprowadza się do: określenia kształtu pożądanej odpowiedzi częstotliwościowej, zaprojektowania filtra analogowego, wyznaczenia jego odpowiedzi, wykonania próbkowania tej odpowiedzi a próbki te decydują o poszukiwanych współczynnikach filtra. Należy tutaj pamiętać o \textbit{aliasingu} zniekształcającym takie działanie. Badanie stabilności filtra może być realizowane na wykresie biegunowym (Zero-Pole-Gain) tworzonym z przestrzeni częstotliwościowej
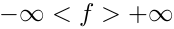 za pomocą transformacji dwuliniowej. Funkcja odpowiedzi impulsowej filtra IIR będzie zanikała (gdy bieguny będą wewnątrz koła jednostkowego), będzie ustabilizowana (bieguny w kole jednostkowym) lub rozbieżna (bieguny na zewnątrz koła). Wadą wykresu biegunowego (w porównaniu do wykresu 'moduł-faza') jest brak odwzorowania charakterystyk przejściowych filtrów.
za pomocą transformacji dwuliniowej. Funkcja odpowiedzi impulsowej filtra IIR będzie zanikała (gdy bieguny będą wewnątrz koła jednostkowego), będzie ustabilizowana (bieguny w kole jednostkowym) lub rozbieżna (bieguny na zewnątrz koła). Wadą wykresu biegunowego (w porównaniu do wykresu 'moduł-faza') jest brak odwzorowania charakterystyk przejściowych filtrów.